Рекурсия и итерация (RU)
Когда мы начинаем познавать азы программирования, как правило первой написанной нами является программа, печатающая строку «Hello, world!». Потом знакомятся с переменными, операторами, функциями. И как правило, первыми, с которыми начинает знакомиться новичок, являются условный оператор и оператор цикла. Сразу же появляется желание написать какую-нибудь простую функцию: факториал числа, возведение в степень или вычисление биномиального коэффициента. При этом в большинстве случаев начинающий программист реализует итеративный вариант функций. Однако мало кто знает, что любую итеративную функцию можно реализовать и рекурсивно.
Рекурсией называется такой способ организации обработки данных, при котором программа (или функция) вызывает сама себя или непосредственно, или из других программ (функций).
Функция называется рекурсивной, если во время ее обработки возникает ее повторный вызов, либо непосредственно, либо косвенно, путем цепочки вызовов других функций.
 Итерацией называется такой способ организации обработки данных, при котором некоторые действия многократно повторяются, не приводя при этом к рекурсивным вызовам программ (функций).
Итерацией называется такой способ организации обработки данных, при котором некоторые действия многократно повторяются, не приводя при этом к рекурсивным вызовам программ (функций).
Теорема. Произвольный алгоритм, реализованный в рекурсивной форме, может быть переписан в итерационной форме и наоборот.
Далее рассмотрим набор элементарных функций, реализованных как при помощи операторов цикла, так и при помощи рекурсивного подхода. Перед написанием рекурсивных функций на любом языке программирования, как правило, необходимо записать рекуррентное соотношение, определяющее метод вычисления функций. Рекуррентное соотношение должно содержать как минимум два условия:
I) условие продолжения рекурсии (шаг рекурсии);
II) условие окончания рекурсии.
Рекурсию будем реализовывать посредством вызова функции самой себя. При этом в теле функции сначала следует проверять условие продолжения рекурсии. Если оно истинно, то выходим из функции. Иначе совершаем рекурсивный шаг.
Итеративный вариант функций будем реализовывать при помощи оператора цикла for.
1. Факториал числа. Факториалом целого неотрицательного числа n называется произведение всех натуральных чисел от 1 до n и обозначается n!. Если f(n) = n!, то имеет место рекуррентное соотношение:
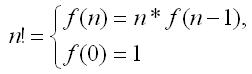
Первое равенство описывает шаг рекурсии – метод вычисления f(n) через f(n – 1). Второе равенство указывает, когда при вычислении функции следует остановиться. Если его не задать, то функция будет работать бесконечно долго.
Например, значение f(3) можно вычислить следующим образом:
f(3) = 3 · f(2) = 3 · 2 · f(1) = 3 · 2 · 1 · f(0) = 3 · 2 · 1 · 1 = 6
Очевидно, что при вычислении f(n) следует совершить n рекурсивных вызовов.
рекурсивная реализация | циклическая реализация |
int f(int n) { if (!n) return 1; return n * f(n - 1); }
| int f(int n) { int i, res = 1; for (i = 1; i <= n; i++) res = res * i; return res; } |
Идея циклической реализации состоит в непосредственном вычислении факториала числа при помощи оператора цикла:
f(n) = 1 · 2 · 3 · … · n
2. Степень числа за линейное время. Вычисление степени числа f(a, n) = an с линейной (O(n)) временной оценкой можно определить при помощи следующего рекуррентного соотношения:
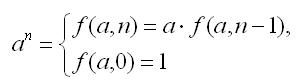
рекурсивная реализация | циклическая реализация |
int f(int a, int n) { if (!n) return 1; return a * f(a, n - 1); }
| int f(int a, int n) { int i, res = 1; for (i = 0; i < n; i++) res = res * a; return res; } |
В итерационном варианте достаточно вычислить произведение a · a · … · a (n множителей a).
3. Степень числа за логарифмическое время. Вычисление степени числа f(a, n) = an с временной оценкой O(log2n) определим следующим образом:
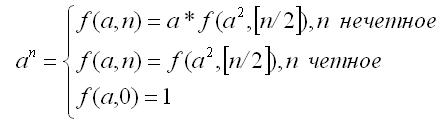
Например, возведение в десятую степень можно реализовать так:
![]()
Поскольку возведение в квадрат эквивалентно одному умножению, то для вычисления a10 достаточно совершить 4 умножения.
рекурсивная реализация | циклическая реализация |
int f(int a, int n) { if (!n) return 1; if (n & 1) return a * f(a * a, n / 2); return f(a * a, n / 2); }
| int f(int a, int n) { int res = 1; while (n > 0) { if (n & 1) res *= a; n >>= 1; a *= a; } return res; } |
4. Сумма цифр числа. Сумму цифр натурального числа n можно найти при помощи функции f(n), определенной следующим образом:
![]()
Условие продолжения рекурсии: сумма цифр числа равна последней цифре плюс сумма цифр числа без последней цифры (числа, деленного нацело на 10).
Условие окончания рекурсии: Если число равно 0, то сумма его цифр равна 0.
Например, сумма цифр числа 234 будет вычисляться следующим образом:
f(234) = 4 + f(23) = 4 + 3 + f(2) = 4 + 3 + 2 + f(0) = 4 + 3 + 2 + 0 = 9
рекурсивная реализация | циклическая реализация |
int f(int n) { if (!n) return 0; return n % 10 + f(n / 10); }
| int f(int n) { int res = 0; for (; n>0; n = n / 10) res = res + n % 10; return res; } |
5. Число единиц. Количество единиц в двоичном представлении числа n можно вычислить при помощи функции f(n), определенной следующим образом (& - операция побитового 'И'):
![]()
В результате операции n = n & (n – 1) уничтожается последняя единица в двоичном представлении числа n:
n = a1a2…ak-1ak10…0
n – 1 = a1a2…ak-1ak01…1
n & (n – 1) = a1a2…ak-1 000…0
Рекурсивный вызов функции f будет совершаться столько раз, сколько единиц в двоичном представлении числа n.
рекурсивная реализация | циклическая реализация |
int f(int n) { if (!n) return 0; return 1 + f(n & (n - 1)); }
| int f(int n) { int res = 0; for (; n > 0; n = n & (n - 1)) res++; return res; } |
6. Биномиальный коэффициент. Значение биномиального коэффициента равно
![]()
и определяется рекуррентным соотношением:
![]()
int c(int k, int n)
{
if (n == k) return 1;
if (k == 0) return 1;
return c(k - 1, n - 1) + c(k, n - 1);
}
Учитывая, что
![]()
значение биномиального коэффициента можно вычислить при помощи цикла. При этом все операции деления будут целочисленными. Если k > n – k, то следует воспользоваться соотношением
![]()
во избежании Time Limit при вычислении, например, значения
![]()
int Cnk(int k, int n)
{
long long res = 1;
if (k > n - k) k = n - k;
for (int i = 1; i <= k; i++)
res = res * (n - i + 1) / i;
return (int)res;
}
7. Рекурсивная функция. Для заданного натурального n вычислим значение функции f(n), заданной рекуррентными соотношениями:
f(2 · n) = f(n),
f(2 · n + 1) = f(n) + f(n + 1),
f(0) = 0, f(1) = 1
Непосредственная реализация функции f(n) имеет вид:
int f(int n)
{
if (n <= 1) return n;
if (n % 2) return f(n / 2) + f(n / 2 + 1);
return f(n / 2);
}
При такой реализации некоторые значения функции f могут вычисляться несколько раз. Рассмотрим другой подход к вычислению значений f. Определим функцию
g(n, i, j) = i · f(n) + j · f(n + 1),
для которой имеют место равенства:
g(2·n, i, j) = g(n, i + j, j),
g(2·n + 1, i, j) = g(n, i, i + j),
g(0, i, j) = i · f(0) + j · f(1) = j
Используя приведенные соотношения, можно вычислить значение f(n) = g(n, 1, 0) с временной оценкой O(log n).
int g(int n, int i, int j)
{
if (!n) return j;
if (n % 2) return g(n / 2, i, i + j);
return g(n / 2, i + j, j);
}
int f(int n)
{
return g(n, 1, 0);
}
8. Функция Аккермана. Функция Аккермана A(m, n) определяется рекурсивно следующим образом:
A(0, n) = n + 1,
A(m, 0) = A(m – 1, 1),
A(m, n) = A(m – 1, A(m, n – 1))
Рекурсивная реализация функции Аккермана имеет вид:
int a(int m, int n)
{
if (!m) return n + 1;
if (!n) return a(m - 1, 1);
return a(m - 1, a(m, n - 1));
}
Для малых значений m функцию Аккермана можно выразить явно:
A(0, n) = n + 1
A(1, n) = 2 + (n + 3) – 3 = n + 2
A(2, n) = 2 · (n + 3) – 3 = 2 · n + 3
A(3, n) = 2n + 3 – 3
9. Отбор в разведку [ACM, 1999]. Из n солдат, выстроенных в шеренгу, требуется отобрать нескольких в разведку. Для совершения этого выполняется следующая операция: если солдат в шеренге больше чем 3, то удаляются все солдаты, стоящие на четных позициях, или все солдаты, стоящие на нечетных позициях. Эта процедура повторяется до тех пор, пока в шеренге останется 3 или менее солдат. Их и отсылают в разведку. Вычислить количество способов, которыми таким образом могут быть сформированы группы разведчиков ровно из трех человек.
Вход. Количество солдат в шеренге n ( 0 < n ≤ 107).
Выход. Количество способов, которыми можно отобрать солдат в разведку описанным выше способом.
Пример входа | Пример выхода |
10 | 2 |
4 | 0 |
Решение. Обозначим через f(n) количество способов, которыми можно сформировать группы разведчиков из n человек в шеренге. Поскольку нас интересуют только группы по три разведчика, то f(1) = 0, f(2) = 0, f(3) = 1. То есть из трех человек можно сформировать только одну группу, из одного или двух – ни одной.
Если n четное, то применяя определенную в задаче операцию удаления солдат в шеренге, мы получим в качестве оставшихся либо n / 2 солдат, стоящих на четных позициях, либо n / 2 солдат, стоящих на нечетных позициях. То есть f(n) = 2 · f(n / 2) при четном n.
Если n нечетное, то после удаления останется либо n / 2 солдат стоявших на четных позициях, либо n / 2 + 1 солдат, стоявших на нечетных позициях. Общее количество способов при нечетном n равно
f(n) = f(n / 2) + f(n / 2 + 1).
Таким образом, получена рекуррентная формула для вычисления значения f(n):
f(n) = 2 · f(n / 2), если n четное
f(n) = f(n / 2) + f(n / 2 + 1), если n нечетное
f(1) = 0, f(2) = 0, f(3) = 1
Реализация функции f имеет вид:
int f(int n)
{
if (n <= 2) return 0;
if (n == 3) return 1;
if (n % 2) return f(n / 2) + f(n / 2 + 1);
return 2 * f(n / 2);
}
10. Большой модуль [Вальядолид, 374]. По заданным b, p, m вычислить значение выражения bp mod m.
Вход. Содержит несколько тестов. Числа b, p, m находятся в отдельных строках. Известно, что 0 ≤ b, p ≤ 2147483647, 1 ≤ m ≤ 46340.
Выход. Для каждого теста вывести в отдельной строке значение bp mod m.
Пример входа | Пример выхода |
3 | 13 |
18132 | 2 |
17 | 13195 |
| |
17 |
|
1765 |
|
3 |
|
| |
2374859 |
|
3029382 |
|
36123 |
|
Решение. Из ограничений на входные данные следует, что в процессе вычисления достаточно использовать тип данных int. Возведение в степень bp будем производить с логарифмической временной сложностью O(log p) используя алгоритм, базирующийся на двоичном разложении показателя степени p:

Пример. Для вычисления значения из первого теста 318132 (mod 17) следует представить показатель степени в двоичной системе исчисления: 1813210 = 1000110110101002. Далее
318132 (mod 17) = 316384 · 31024 · 3512 · 3128 · 364 · 316 · 34 (mod 17) = 13.
Для второго теста 171765 (mod 3) = (17 mod 3) 1765 (mod 3) = 2 1765 (mod 3) = 2.
11. Истина, спрятанная в рекуррентности [Вальядолид, 10547]. Функция f определена следующим образом:
f(0, 0) = 1,
f(n, r) = ![]() , если n > 0 и 0 ≤ r ≤ n(k – 1) + 1,
, если n > 0 и 0 ≤ r ≤ n(k – 1) + 1,
f(n, r) = 0 иначе.
Вычислить значение x = ![]() , где m = 10t.
, где m = 10t.
Например, значения f(n, i) при k = 3 имеют вид (в пустых клетках стоят нули):
n \ i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
0 | 1 |
|
|
|
|
|
|
|
|
1 | 1 | 1 | 1 |
|
|
|
|
|
|
2 | 1 | 2 | 3 | 2 | 1 |
|
|
|
|
3 | 1 | 3 | 6 | 7 | 6 | 3 | 1 |
|
|
4 | 1 | 4 | 10 | 16 | 19 | 16 | 10 | 4 | 1 |
Вход. На вход подается не более 1001 тестов. Каждая строка содержит три целых числа: k, n и t (0 < k, n < 1019, 0 < t < 10). Последний тест содержит k = n = t = 0 и не обрабатывается.
Выход. Для каждого теста вместе с его номером в отдельной строке вывести значение x.
Пример входа | Пример выхода |
1234 1234 4 | Case #1: 736 |
2323 99999999999 8 | Case #2: 39087387 |
4 99999 9 | Case #3: 494777344 |
888 888 8 | Case #4: 91255296 |
0 0 0 |
|
Решение. Рассмотрим все n - цифровые числа в системе исчисления с основанием k (включая числа с ведущими нулями). Общее их количество равно kn. Пусть f(n, r) – количество таких чисел, сумма цифр которых равна r. Тогда
f(n, r) = f(n – 1, r) + f(n – 1, r – 1) + … + f(n – 1, r – k + 1) =
Минимальная сумма цифр для таких чисел равна 0, максимальная (k – 1) * n. Просуммировав значения f(n, r) для r от 0 до (k – 1) * n, получим общее количество n - цифровых чисел в системе исчисления с основанием k, то есть kn.
Таким образом x = kn (mod 10t). Поскольку t < 10, то при вычислении модулярной экспоненты достаточно использовать 64-битный целочисленный тип.
Пример. Для первого теста имеет место равенство: 12341234 (mod 104) = 736.
12. f91 [Вальядолид, 10696]. Вычислить значение функции f91, заданной рекуррентным соотношением:
![]()
Вход.Каждая входная строка содержит натуральное число n (n ≤ 1000000). Число n = 0 является концом входных данных и не обрабатывается.
Выход. Для каждого входного n вывести значение f91(n) как показано в примере ниже.
Пример входа | Пример выхода |
500 | f91(500) = 490 |
91 | f91(91) = 91 |
0 |
|
Решение. Сначала вычислим значения функции f91(n) для n ≤ 100. Например:
f91(100) = f91(f91(111)) = f91(101) = 91, f91(99) = f91(f91(110)) = f91(100) = 91
Аналогично продолжая, можно заметить что f91(n) = 91, где 1 ≤ n ≤ 100. Таким образом, имеет место соотношение:
![]()
13. Повторяющийся Иосиф [Вальядолид, 10774]. По кругу стоят n людей, занумерованных от 1 до n. Начиная отсчет с первого и двигаясь по кругу, будем казнить каждого второго человека до тех пор пока не останется один. Пусть этот выживший имеет номер x. Расставим по кругу x людей и повторим процедуру, после которой выживет человек с номером y. И так далее до тех пор, пока номер выжившего не станет равным первоначальному количеству людей в текущем раунде.
Например, при n = 5 последовательно будут казнены 2, 4, 1, 5. Выживет номер 3. Он не равен 5 (количеству людей в раунде), поэтому следует повторить процедуру. Для n = 3 казнены будут 2, 1. Выживет человек с номером 3, равным n. Процедура заканчивается.
Вход. Первая строка содержит количество тестов. Каждый тест в отдельной строке содержит одно число n (0 < n £ 30000)
Выход. Для каждого теста вывести в отдельной строке его номер как указано в примере, количество повторений процедуры казни после первой итерации и номер выжившего в конце процедуры.
Пример входа | Пример выхода |
2 | Case 1: 2 7 |
13 | Case 2: 8 1023 |
23403 |
|
Решение. Пусть n – количество людей в круге. Обозначим через f(n) номер последнего уцелевшего. Положим f(1) = 1.
Если n = 2 · k – четное, то после прохода первого круга будут удалены люди с четными номерами: 2, 4, ..., 2 · k. Останутся люди с нечетными номерами, а отсчет продолжаем с номера 1. Это все равно, что если бы у нас было k людей, а номер каждого удвоился и уменьшился на 1. То есть получим соотношение f(2 · k) = 2 · f(k) – 1.

Если n = 2·k + 1 – нечетное, то после прохода первого круга будут удалены люди с четными номерами 2, 4, ..., 2·k, а жертва с номером 1 уничтожается сразу же после жертвы с номером 2·k. Остается k людей с номерами 3, 5, 7, …, 2·k + 1. Это все равно, что люди занумерованы от 1 до k, только номер каждого удвоился и увеличился на 1. Получаем соотношение: f(2·k + 1) = 2·f(k) + 1.

Объединяя полученные соотношения, получим рекуррентность:
f(1) = 1
f(2·k) = 2·f(k) – 1, k ≥ 1
f(2·k + 1) = 2·f(k) + 1, k ≥ 1
Теорема. Значение f(n) получается путем циклического сдвига двоичного представления n влево на один бит. Например, f(100) = f(11001002) = 10010012 = 73.
Многократное применение функции f порождает последовательность убывающих значений, достигающих неподвижной точки n такой что f(n) = n. Число n будет состоять из одних единиц со значением 2v(n) – 1, где v(n) – количество единиц в бинарном представлении числа n.
Пример.Рассмотрим входные данные для второго теста. При n = 13 последовательно будут казнены 2, 4, 6, 8, 10, 12, 1, 5, 9, 13, 7, 3. Выживет номер 11. Он не равен 13 (количеству людей в раунде), поэтому следует повторить процедуру. Для n = 11 казнены будут 2, 4, 6, 8, 10, 1, 5, 9, 3, 11. Выживет человек с номером 7, равным n. При n = 7 выживет номер 7. После первой итерации проведено еще 2 повторения процедуры казни.
14. Простое сложение [Вальядолид, 10994]. Определим рекурсивную функцию f(n) следующим образом:

Определим функцию S(p, q) следующим образом:
![]()
В задаче необходимо вычислить значение S(p, q) по заданным p и q.
Вход. Каждая строка содержит два неотрицательных 32-битовых знаковых числа p и q (p £ q). Последняя строка содержит два отрицательных целых числа и не обрабатывается.
Выход. Для каждой пары p и q вывести значение S(p, q).
Пример входа | Пример выхода |
1 10 | 46 |
10 20 | 48 |
30 40 | 52 |
-1 -1 |
|
Решение. Приведенная в условии функция f(n) находит последнюю ненулевую цифру числа n. Обозначим через
g(p) = ![]() Тогда S(p, q) = g(q) – q(p – 1). Для вычисления функции g(p), суммы последних значащих цифр для чисел от 1 до p, разобьем числа от 1 до p на три множества (операция деления ‘/’ является целочисленной):
Тогда S(p, q) = g(q) – q(p – 1). Для вычисления функции g(p), суммы последних значащих цифр для чисел от 1 до p, разобьем числа от 1 до p на три множества (операция деления ‘/’ является целочисленной):
1. Числа от (p / 10)·10 + 1 до p;
2. Числа от 1 до (p / 10)·10, не оканчивающиеся нулем;
3. Числа от 1 до (p / 10)·10, оканчивающиеся нулем;
Например, при p = 32 к первому множеству отнесутся числа 31, 32, ко второму 1, …, 9, 11, …, 19, 21, …, 29, к третьему 10, 20.
Сумма последних значащих цифр в первом множестве равна 1 + 2 + … + p%10 = t(1 + t) / 2, где t = p % 10. Во втором множестве искомая сумма равна p / 10·45, так как сумма всех цифр от 1 до 9 равна 45, а число полных десятков равно p / 10. Требуемую сумму для третьего множества найдем рекурсивно: она равна g(p / 10).
Достаточно большое число олимпиадных задач требует написания рекурсивных функций или циклической реализации. Например,
[Вальядолид] http://acm.uva.es/problemset: 374 (Большой модуль), 10547 (Истина, спрятанная в рекуррентности), 10696 (f91), 10774 (Повторяющийся Иосиф), 10994 (Простое сложение).
СПИСОК ЛИТЕРАТУРЫ
1. "Алгоритмы построение и анализ", Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К., – Москва, Санкт-Петербург, Киев, 2005 – 1292 с.
2. "Практика и теория программирования", Книга 2. Винокуров Н.А., Ворожцов А.В., – М: Физматкнига, 2008 - 288 с.
